Introduction

I am in progress of creating a game where a team of game characters will seek out its nearest enemy in a grid setup. There are a lot of ways how this can be achieved. For example, one of the common ways is to keep track of all the enemies in a list and loop through the list to get the nearest enemy. But this is not feasible for me as this will be a multi-player game which means there is a lot of permutation of character vs enemy(each player team’s enemy is everyone else group of game characters). So I have decided to do it via checking surrounding grids and expanding outwards.

Preparation

To aid with this setup, I have a 2D list to store the position. As illustrated below(simplified) we can see that if the grid is occupied, it will be marked as a number other than zero. Zero means it is unoccupied. Different numbers mean they are enemy of one another. For example, a grid that contains 2 holds the enemy of the characters residing in the grid value containing 1 and vice versus.

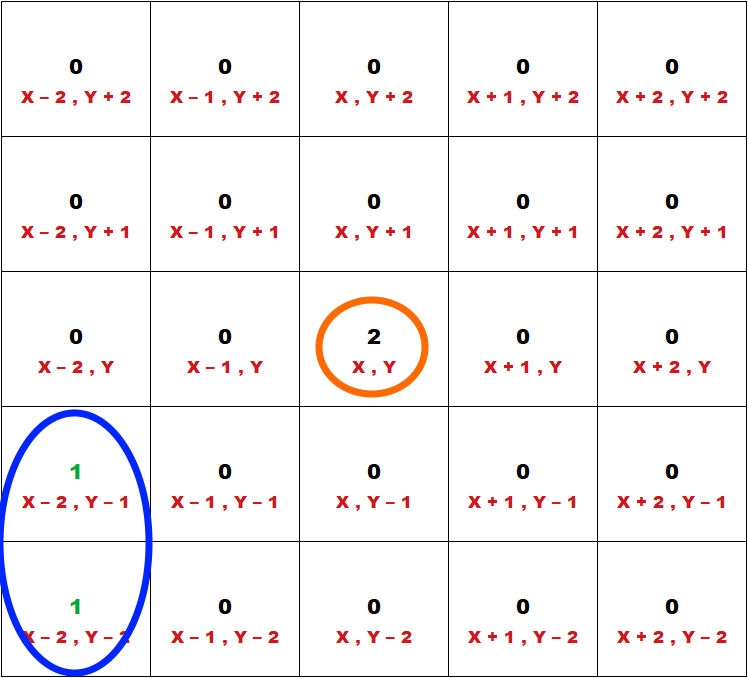
Explanation of the program

1st Layer of surrounding grids

Let’s see how we are going to write the program starting with finding the pattern of the surrounding grids. We will begin with the first layer of surrounding grids and move out from there.

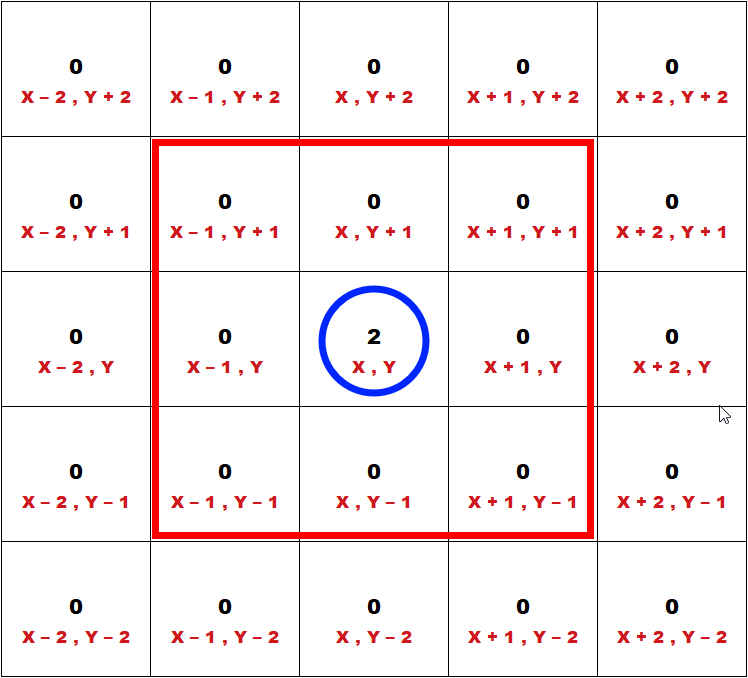
Let’s take the grid we are going to find its surrounding grids to be X , Y. So the surrounding grids will be:

  1. X - 1 , Y + 1
  2. X - 1 , Y
  3. X - 1 , Y - 1
  4. X , Y + 1
  5. X , Y - 1
  6. X + 1 , Y + 1
  7. X + 1 , Y
  8. X + 1 , Y - 1

If you see the list of surrounding grids it is all of the combinations +1 and -1.
In cases where are +0 (or nothing added/subtracted on X or Y), the other dimension will either be with a + 1 or - 1 (for example X, Y -1 or X + 1, Y).
And there is only addition and subtraction of one, not two or more.
So we can deduce that the addition and subtraction are in correspond to its layer. Let’s call this layer number as layerNumber. So by substituting the + 1 and -1 with layerNumber we will get:

  1. X - layerNumber , Y + layerNumber
  2. X - layerNumber , Y
  3. X - layerNumber , Y - layerNumber
  4. X , Y + layerNumber
  5. X , Y - layerNumber
  6. X + layerNumber , Y + layerNumber
  7. X + layerNumber , Y
  8. X + layerNumber , Y - layerNumber

2nd layer of surrounding grids

Now is the exciting part when we get to the second layer.

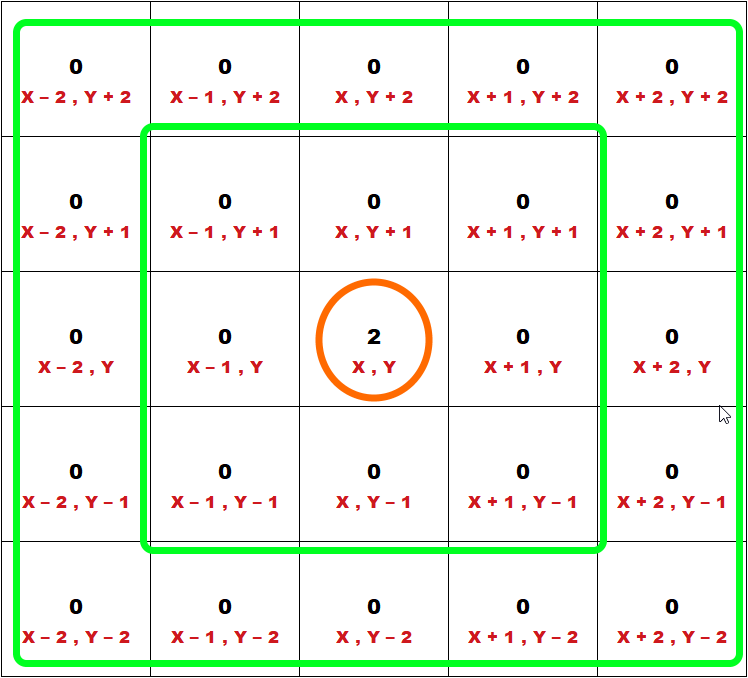
We can now see the surrounding grids to be:

  1. X - 2 , Y + 2
  2. X - 2 , Y + 1
  3. X - 2 , Y
  4. X - 2 , Y - 1
  5. X - 2 , Y - 2
  6. X - 1 , Y + 2
  7. X - 1 , Y - 2
  8. X , Y + 2
  9. X , Y - 2
  10. X + 1 , Y + 2
  11. X + 1 , Y - 2
  12. X + 2 , Y + 2
  13. X + 2 , Y + 1
  14. X + 2 , Y
  15. X + 2 , Y - 1
  16. X + 2 , Y - 2

Phew!! Much more than the 1st layer. Now we can see more combination of addition and subtraction. But the pattern we can see now even if there is a decrement of the addition or subtraction factor, the other dimension will always be an addition or subtraction of the layer number. So let’s substitute the values of addition and subtractions which are lower than the layer number(if layer number is 2 so the values will be 1 and 0) as decValue and the values of addition and subtractions that are corresponding with the layer number as layerNumber:

  1. X - layerNumber , Y + layerNumber
  2. X - layerNumber , Y + decValue
  3. X - layerNumber , Y +/- decValue
  4. X - layerNumber , Y - decValue
  5. X - layerNumber , Y - layerNumber
  6. X - decValue , Y + layerNumber
  7. X - decValue , Y - layerNumber
  8. X +/- decValue , Y + layerNumber
  9. X +/- decValue , Y - layerNumber
  10. X + decValue , Y + layerNumber
  11. X + decValue , Y - layerNumber
  12. X + layerNumber , Y + layerNumber
  13. X + layerNumber , Y + decValue
  14. X + layerNumber , Y +/- decValue
  15. X + layerNumber , Y - decValue
  16. X + layerNumber , Y - layerNumber

Note that those which do not have addition or subtraction values are replaced with +/- decValue because they are still part of decValue(0 is smaller than the layer Number), it is just that we do not know if it is addition and subtraction so we will put both addition and subtraction symbol to it. Now let’s rearrange the list so that those with only layer Numbers will group together.

  1. X - layerNumber , Y + layerNumber
  2. X - layerNumber , Y - layerNumber
  3. X + layerNumber , Y + layerNumber
  4. X + layerNumber , Y - layerNumber
  5. X - layerNumber , Y + decValue
  6. X - layerNumber , Y - decValue
  7. X + layerNumber , Y + decValue
  8. X + layerNumber , Y - decValue
  9. X - decValue , Y + layerNumber
  10. X - decValue , Y - layerNumber
  11. X + decValue , Y + layerNumber
  12. X + decValue , Y - layerNumber
  13. X +/- decValue , Y + layerNumber
  14. X +/- decValue , Y - layerNumber
  15. X - layerNumber , Y +/- decValue
  16. X + layerNumber , Y +/- decValue

Forming the program (Part 1)

The first part is for those which only have layer number for addition and subtraction(1-4), this code will be as below:

for layerNumber in range(1,maxNumberOfLayers):
    if (contains_enemy(X - layerNumber, Y + layerNumber)) list.add(X - layerNumber, Y + layerNumber)
    if (contains_enemy(X - layerNumber, Y - layerNumber)) list.add(X - layerNumber, Y - layerNumber)
    if (contains_enemy(X + layerNumber, Y + layerNumber)) list.add(X + layerNumber, Y + layerNumber)
    if (contains_enemy(X + layerNumber, Y - layerNumber)) list.add(X + layerNumber, Y - layerNumber)
    if (len(list)>0) break

The above is to loop through all the possible layers starting from the 1st and check the corresponding neighbor grid if it contains enemy(simplified as a function named contains_enemy), if it is true it will add to a list. Then exit the for loop if anything is added to the list as we only need to get the nearest enemies list which is the nearest possible layer away from the character.

Forming the program (Part 2)

Next is handle those with the decValues(5-12). Since decValues are values lower than that of the layerNumber, we can use a for loop based on what is in the layerNumber.

for layerNumber in range(1,maxNumberOfLayers):
    for decValue in range(layerNumber):
        if (contains_enemy(X - layerNumber, Y + decValue)) list.add(X - layerNumber, Y + decValue)
        if (contains_enemy(X - layerNumber, Y - decValue)) list.add(X - layerNumber, Y - decValue)
        if (contains_enemy(X + layerNumber, Y + decValue)) list.add(X + layerNumber, Y + decValue)
        if (contains_enemy(X + layerNumber, Y - decValue)) list.add(X + layerNumber, Y - decValue)
        if (contains_enemy(X - decValue, Y + layerNumber)) list.add(X - decValue, Y + layerNumber)
        if (contains_enemy(X - decValue, Y - layerNumber)) list.add(X - decValue, Y - layerNumber)
        if (contains_enemy(X + decValue, Y + layerNumber)) list.add(X + decValue, Y + layerNumber)
        if (contains_enemy(X + decValue, Y - layerNumber)) list.add(X + decValue, Y - layerNumber)
    if (len(list)>0) break

Forming the program (Part 3)

Of course, I have yet to add in the part where decValue is equal to zero(13-16) to the code. There is no need to because it is already in the code(0 for decValue is stated as +/- decValue, I have already have + decValue and -decValue in the code). But you will notice there will be an issue if decValue is 0. There will be duplicates because if decValue is 0, X + decValue will be equal to X - decValue, same for Y. So we will need to sacrifice a set of the equations(e.g choose one from X + decValue and X - decValue) to be omitted if decValue is equal to zero to prevent duplication. Being a positive guy, I have decided to sacrifice the negative equations(those with subtraction). So this will be the end result:

for layerNumber in range(1,maxNumberOfLayers):
    for decValue in range(layerNumber):
        if (contains_enemy(X - layerNumber, Y + decValue)) list.add(X - layerNumber, Y + decValue)
        if (contains_enemy(X + decValue, Y + layerNumber)) list.add(X + decValue, Y + layerNumber)
        if (contains_enemy(X + decValue, Y - layerNumber)) list.add(X + decValue, Y - layerNumber)
        if (contains_enemy(X + layerNumber, Y + decValue)) list.add(X + layerNumber, Y + decValue)
        if (decValue != 0):
            if (contains_enemy(X - layerNumber, Y - decValue)) list.add(X - layerNumber, Y - decValue)
            if (contains_enemy(X + layerNumber, Y - decValue)) list.add(X + layerNumber, Y - decValue)
            if (contains_enemy(X - decValue, Y + layerNumber)) list.add(X - decValue, Y + layerNumber)
            if (contains_enemy(X - decValue, Y - layerNumber)) list.add(X - decValue, Y - layerNumber)
    if (len(list)>0) break

Forming the program (Finale)

Now to merge everything, we have:

for layerNumber in range(1,maxNumberOfLayers):
    if (contains_enemy(X - layerNumber, Y + layerNumber)) list.add(X - layerNumber, Y + layerNumber)
    if (contains_enemy(X - layerNumber, Y - layerNumber)) list.add(X - layerNumber, Y - layerNumber)
    if (contains_enemy(X + layerNumber, Y + layerNumber)) list.add(X + layerNumber, Y + layerNumber)
    if (contains_enemy(X + layerNumber, Y - layerNumber)) list.add(X + layerNumber, Y - layerNumber)
    for decValue in range(layerNumber):
        if (contains_enemy(X - layerNumber, Y + decValue)) list.add(X - layerNumber, Y + decValue)
        if (contains_enemy(X + decValue, Y + layerNumber)) list.add(X + decValue, Y + layerNumber)
        if (contains_enemy(X + decValue, Y - layerNumber)) list.add(X + decValue, Y - layerNumber)
        if (contains_enemy(X + layerNumber, Y + decValue)) list.add(X + layerNumber, Y + decValue)
        if (decValue != 0):
            if (contains_enemy(X - layerNumber, Y - decValue)) list.add(X - layerNumber, Y - decValue)
            if (contains_enemy(X + layerNumber, Y - decValue)) list.add(X + layerNumber, Y - decValue)
            if (contains_enemy(X - decValue, Y + layerNumber)) list.add(X - decValue, Y + layerNumber)
            if (contains_enemy(X - decValue, Y - layerNumber)) list.add(X - decValue, Y - layerNumber)
    if (len(list)>0) break

Summary

There you have it, the code, not very pythonic, but I believe this better explains how the spiral matrix search is achieved.